变分自编码器（Variational Autoencoder, VAE）

关于自编码器的概念和变分自编码器的实现，可以参考这里。关于变分自编码器的一篇更详细的介绍见这里。

我们记数据点（图像）为$X\in\chi$。$P(X)$：如果$X$像真实图像则概率高，像随机噪声则概率低。

我们考虑数据是由一系列隐变量(记为$z$)生成的。（例如，我们要生成手写数字，我们可以先决定生成的数字$z_1\in\lbrace0,…,9\rbrace$，然后决定笔划的宽度$z_2\in[1.0, 5.0]$，再由$z_1$和$z_2$生成数字$X$，此时$(z_1, z_2)$就是隐变量）

考虑函数$f(z;\theta)$将隐变量$z$映射到$X$（类似于一个“解码器”），我们希望优化函数$f$的参数$\theta$，使得当我们随机取样$z$时，$f(z;\theta)$能尽可能地接近数据集中已有的$X$。（例如，$z=(z_1, z_2)=(5, 1.0)$时，我们希望优化$\theta$使$f(z;\theta)$尽量接近一个手写的细体5）

为了计算数据$ X $存在的概率，我们就可以用$P(X \vert z;\theta)$对$z$积分计算$P(X)$，可以得到：

\[P(X)=\int_{z}P(X \vert z;\theta)P(z)dz\]

这里，我们可以假定$P(X \vert z;\theta)$是一个以$f(z;\theta)$为均值的高斯分布（即$ P(X \vert z;\theta)=N(X \vert f(z;\theta),\sigma^2*I) $，原因与平均场理论有关，也许以后有机会可以深入探讨）。

根据最大似然的思想，接下来我们需要优化参数$\theta$使我们的模型$f(z;\theta)$生成实际数据$X$的概率$P(X)$最大。这里$f(z;\theta)$往往使用多层神经网络实现。（这里$P(z)$的分布是不重要的，为了方便我们可以直接取$P(z)=N(z \vert 0,I)$。因为只要$f(z;\theta)$足够强，$N(z \vert 0,I)$可以被扭转成任何分布）

在机器学习中，我们将$P(X)$对$ \theta $求导+梯度法来优化。然而，如何计算$ P(X) $？

直接的方法是对$ z $在$ P(z) $上大量取样，则$ P(X)\approx \frac{1}{N}\sum_{i}P(x \vert z_i)$。问题是在高维空间中$ n $需要非常巨大才能得到对$ P(X) $的准确估计。然而注意到，$P(X \vert z;\theta)=N(X \vert f(z;\theta),\sigma^2*I)$，即$ \log P(X \vert z;\theta) $和$ X $与分布均值$ f(z;\theta) $的距离平方$ \Vert X-f(z;\theta) \Vert ^2 $成反比。也就是说，对于大部分的z，$ P(X \vert z;\theta) $都很小。

因此，我们需要一个新的函数$ Q(z \vert X) $，给定一个$ X $，估计一个$ z $的分布，即这个$ z $有多大的概率能产生$ X $（真实的$ P(z \vert X) $难以计算，我们只能估计，即近似推断，approximate inference，详见PRML第10章）。这样的话，我们对$ z $在$ Q(z \vert X) $上取样计算$ P(X)\approx \frac{1}{N}\sum_{i}P(x \vert z_i)$，即$ E_{z \sim Q}P(X \vert z) $，要比直接在$ P(X) $上取样要更加容易。

接下来，$ E_{z \sim Q}P(X \vert z) $和$ P(X) $的关系是变分贝叶斯方法的基础。

（如果对变分推断(Variational Inference, PRML 10.1节)有所了解，后面的内容理解起来会更加自然。建议阅读：Blei, David M., Alp Kucukelbir, and Jon D. McAuliffe. “Variational inference: A review for statisticians.” arXiv preprint arXiv:1601.00670 (2016).）

刚才考虑了$ z $在$ Q(z \vert X) $上取样和在$ P(z) $两个分布上取样，现在我们考虑$ z $在任意分布$ Q(z) $上取样。

考虑$ P(z \vert X) $和$ Q $的KL距离（记为$ D $）：

\[D[Q(z) \Vert P(z \vert X)] = E_{z \sim Q}[\log Q(z) - \log P(z \vert X)]\]

通过对$ P(z \vert X) $使用贝叶斯公式$ P(z \vert X)=\frac{P(x \vert Z)P(z)}{P(X)} $引入$ P(X) $和$ P(x \vert Z) $：

\[D[Q(z) \Vert P(z \vert X)] = E_{z \sim Q}[\log Q(z) - \log P(X \vert z) - \log P(z)] + \log P(X)\]

移项变换得到： \(\log P(X) - D[Q(z) \Vert P(z \vert X)] = E_{z \sim Q}[\log P(X \vert z)] - D[Q(z) \Vert P(z)]\)

（注意这里等式右边称为evidence lower bound (ELBO)。在变分推断里，我们的目标是要找与$ P(x \vert Z) $最接近的$ Q(z) $（最小化KL距离$ D[Q(z) \Vert P(z \vert X)] $），$ \log P(X) $与$ Q $无关，所以在优化$ Q $的过程中可以看为常数，即目标是最大化ELBO。而在VAE中，我们既要最大化$ P(x \vert Z) $，又要让$ Q(z) $和$ \log P(X) $接近（最小化KL距离），而这同样可以通过最大化ELBO实现）

将任意分布$ Q $换为我们关注的$ Q(z \vert X) $，得：

\[\log P(X) - D[Q(z \vert X) \Vert P(z \vert X)] = E_{z \sim Q}[\log P(X \vert z)] - D[Q(z \vert X) \Vert P(z)]\]

由此，对于给定的$ X $，我们将两个难以计算的目标函数$ P(x \vert Z) $和$ D[Q(z) \Vert P(z \vert X)] $变为易于计算的表达形式：

  • $ E_{z \sim Q}[\log P(X \vert z)] $：在分布$ Q(z \vert X) $上取样一个$ z $即可作为$ E_{z \sim Q}[\log P(X \vert z)] $的近似。
  • $ D[Q(z \vert X) \Vert P(z)] $：取$ Q(z \vert X)=N(z \vert \mu(X; \vartheta), \Sigma(X; \vartheta)) $，回顾$ P(z)=N(0, I) $，即可直接计算$ D[Q(z \vert X) \Vert P(z)] $（两个高斯分布的KL距离，有解析解，具体推导见参考文献）。

注意，这里$ \mu(X; \vartheta) $和$ \Sigma(X; \vartheta) $往往使用多层神经网络实现。

VAE的框架如下：

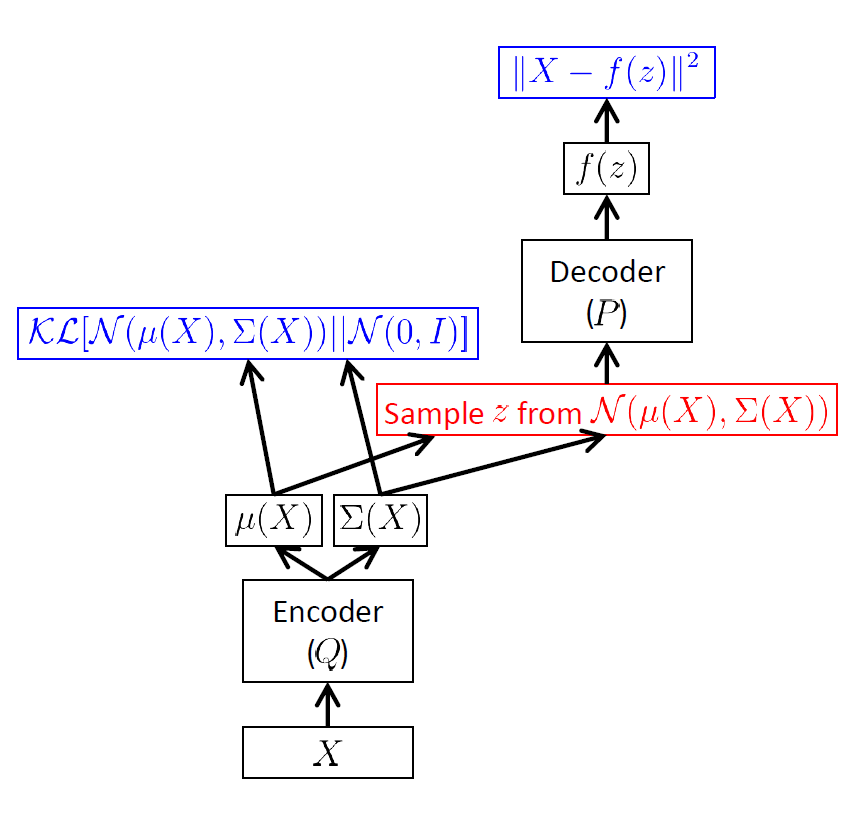
VAE框架-1

这里的$ \Vert X-f(z;\theta) \Vert ^2 $似乎显得陌生（我们不是要最大化$ E_{z \sim Q}[\log P(X \vert z)] $吗？）。然而注意到，对于给定的$ X $，要最大化$ E_{z \sim Q}[\log P(X \vert z)] $，考虑$ P(X \vert z;\theta)=N(X \vert f(z;\theta),\sigma^2*I) $，$ \log P(X \vert z;\theta)= - \frac{1}{2}(X-f(z;\theta))^T (\sigma^2 * I)^{-1} (X-f(z;\theta)) \propto \Vert X-f(z;\theta) \Vert ^2$，即最小化$ \Vert X-f(z;\theta) \Vert ^2 $，两者是等价的。

现在仍然有一个问题：红色部分的取样过程无法计算梯度，如何解决？

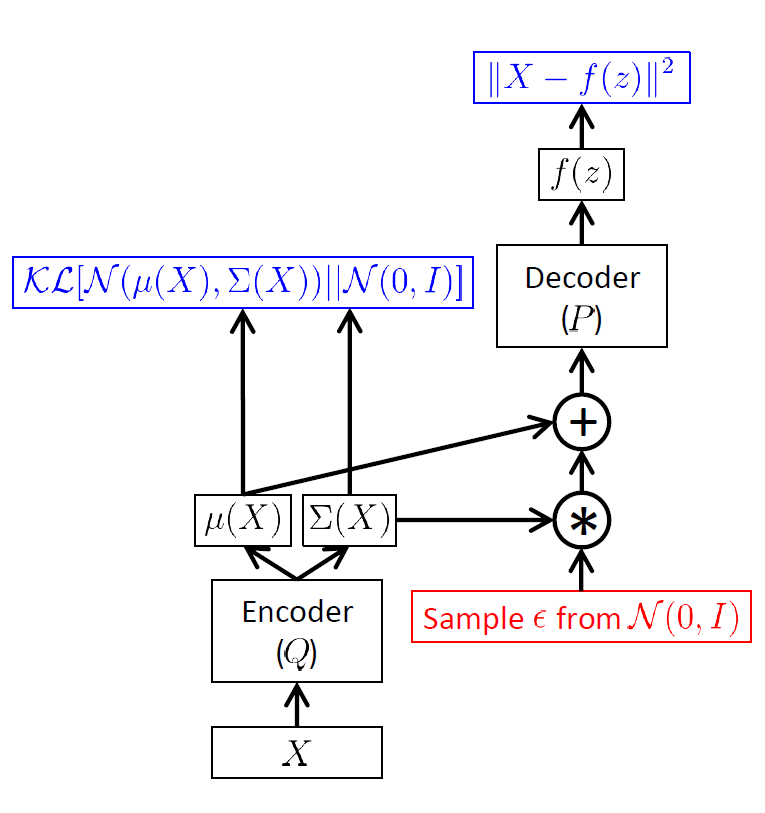
VAE框架-2

我们可以先取样$ \epsilon \sim N(0, I) $，然后$ z=\mu(X) + \Sigma^{1/2}(X) * \epsilon $（即“Reparameterization trick”）

总结VAE流程如下：

  • $ \mu = \mu(X), \Sigma = \Sigma(X) $(通过神经网络进行编码)
  • 取样$ \epsilon \sim N(0, I) $，$ z=\mu + \Sigma^{1/2} * \epsilon $
  • $ f=f(z) $(通过神经网络进行解码)
  • 计算损失函数$ \Vert X-f \Vert ^2 - D[N(\mu,\Sigma \Vert N(0, I)] $
  • 反向传播

参考：