深度信念网络（Deep Belief Networks, DBNs）

深度信念网络（Deep Belief Networks, DBNs）由Geoffrey Hinton于2006年提出，是一种经典的深度生成式模型，通过将一系列受限玻尔兹曼机（RBM）单元堆叠而进行训练。这一模型在MNIST数据集上的表现超越了当时流行的SVM，从而开启了深度学习在学术界和工业界的浪潮，在深度学习的发展历史中具有重要意义。尽管随着大量表现更好的深度学习算法的出现，深度信念网络已经很少使用，但其理论的优美性、方法的开创性和历史意义的重要性使得本文仍将对其进行较细致的介绍。

本文中关于受限玻尔兹曼机（RBM）的部分可参考前一篇文章。

虽然深度信念网络在训练时采取了将一系列受限玻尔兹曼机堆叠的贪心策略，但其本身的结构并非如此。事实上，深度信念网络是由最顶层的一个单层受限玻尔兹曼机加上其下的多层有向的“信念网络”组合而成¹，如下图所示。

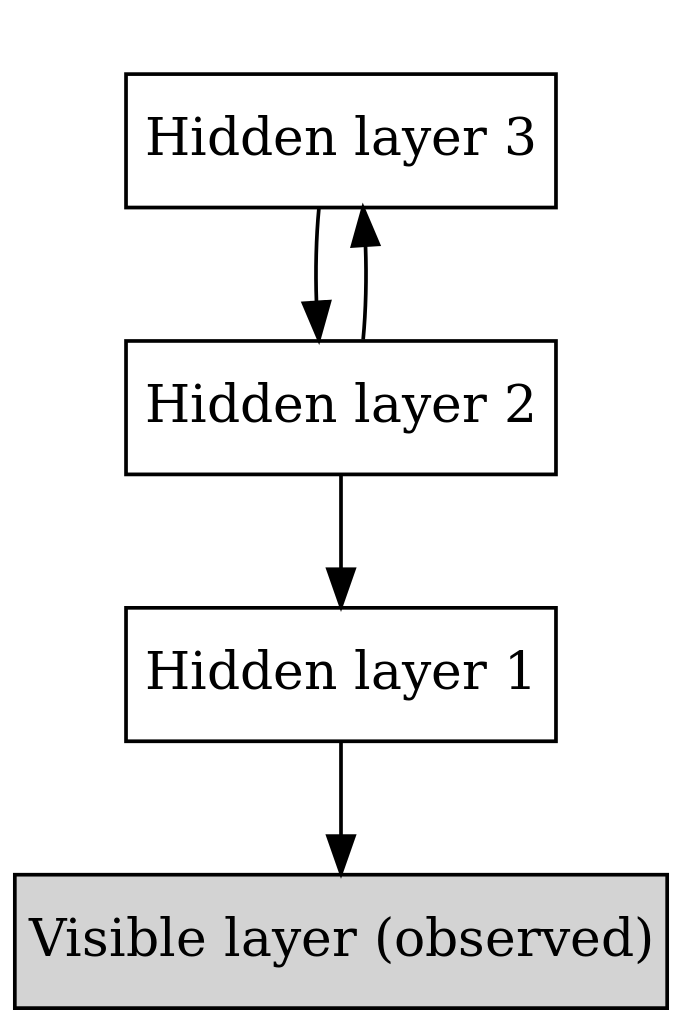
深度信念网络结构图

DBN作为一个生成式模型，我们在了解其原理和训练方法之前，不妨先了解一下如何使用这个模型进行样本的“生成”。假设我们已有一个在MNIST数据集上训练好的$ l $层DBN，现在希望从模型中“生成”一张新的手写体数字图片，步骤如下：

• 从最上层RBM的概率分布（$ P(y_1, y_2, …, y_N) = P(h^{(l-1)}, h^{(l)}) $）中，使用采样方法（一般是Gibbs Sampling²）取一个$ (h^{(l-1)}, h^{(l)}) $；
• 将生成的$ h^{(l-1)} $从上到下经过$ l - 1 $层的信念网络，最终到达可见单元集合v，即为生成的样本。

接下来，介绍DBN的训练算法。与RBM一样，作为无监督的生成式模型，我们的目标是最大化$ P(v) $。在此，DBN提出了“逐层训练”的方式，这一开创性的方法成为深度学习的重要基础。具体而言，从下到上分别将每层信念网络当做RBF进行训练，然后固定当前层权值，取样当前层的“隐层”作为下一层的输入。算法如下：

• 将第一层信念网络视作RBM进行训练，得到权值$ W^{(1)} $；
• 固定权值$ W^{(1)} $，从$ Q(h^{(1)}\vert v) = P(h^{(1)}\vert v, W^{(1)}) $中取样一个$ h^{(1)} $作为训练下一层RBM的输入；
• 将$ h^{(1)} $作为输入， 将第二层信念网络视作RBM进行训练，得到权值$ W^{(2)} $；
• 固定权值$ W^{(2)} $，从$ Q(h^{(2)}\vert v) = P(h^{(2)}\vert h^{(1)}, W^{(2)}) $中取样一个$ h^{(1)} $作为训练下一层RBM的输入；
• 依次逐层训练直到最顶层。

在一般深度学习的讨论中，往往给出算法后就到此为止了，直接进入实验和结果部分。换言之，没有讨论“为什么可以这样做，为什么这样效果更好”的问题。然而深度信念网络却是有一定的理论依据的。接下来简要介绍深度信念网络中逐层训练的原理。以下内容主要基于(Salakhutdinov, 2015)。

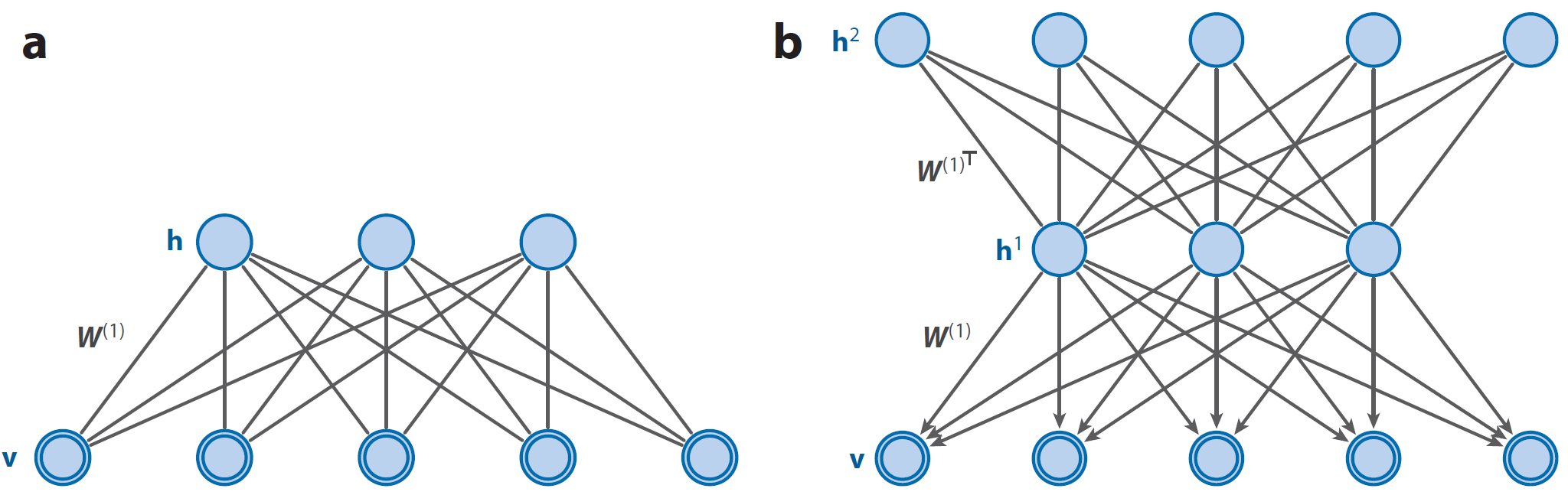
(a)一个玻尔兹曼机（RBM），(b)一个具有两个隐层的深度信念网络（DBN），其中$ W^{(2)} = W^{(1)^T} $。由DBN定义的联合分布$ P(v, h^{(1)}; W^{(1)}) $与RBM定义的联合分布$ P(v, h^{(1)} W^{(1)}) $相等。图片来自(Salakhutdinov, 2015)

首先，如果我们已有一个RBM，我们可以根据这个RBM构造一个两个隐层的DBN，如上图所示。其第一层的结构与权值$ W^{(1)} $均与RBM相同（只不过变成了有向的信念网络），第二层则相当于把RBM“倒过来”，隐层单元数量等于第一层显层单元数量，$ W^{(2)} = W^{(1)^T} $。这个DBN的$ v $，$ h^{(1)} $和$ h^{(2)} $的联合概率分布为：

\[\begin{equation*} P(v, h^{(1)}, h^{(2)}; \theta) = P(v\vert h^{(1)}; W^{(1)})P(h^{(1)}, h^{(2)}; W^{(2)}) \end{equation*}\]

其中，$ \theta = {W^{(1)}, W^{(2)}} $，$ P(v\vert h^{(1)}; W^{(1)}) $是有向信念网络，$ P(h^{(1)}, h^{(2)}; W^{(2)}) $是第二层RBM的联合分布，其计算公式分别为：

\[\begin{align*} P(v\vert h^{(1)}; W^{(1)}) &= \prod_{y_i \in v}p(y_i\vert h^{(1)}; W^{(1)}) \\ P(y_i = 1\vert h^{(1)}; W^{(1)}) &= sigmoid(\sum_{j \in h}W_{ij}^{(1)}h_j^{(1)}) \\ P(h^{(1)}, h^{(2)}; W^{(2)}) &= \frac{1}{Z(W^{(2)})}\exp(h^{(1)^T}W^{(2)}h^{(2)}) \end{align*}\]

逐层训练的贪心策略基于以下两点³：

• DBN在$ v $和$ h^{(1)} $上的联合概率分布$ P(v, h^{(1)}; \theta) = \sum_{h^{(2)}}P(v, h^{(1)}, h^{(2)}; \theta) $和RBM在$ v $和$ h^{(1)} $上的联合概率分布$ P(v, h^{(1)}; W^{(1)}) $相等；
• 两个模型关于$ h^{(1)} $的边缘分布$ P(h^{(1)}\vert W^{(1)}) $也是相同的。

于是，对于一个DBN，我们可以先把最底层当做一个RBM来训练，得到权值参数$ W^{(1)} $，然后将第二层的权重初始化为$ W^{(2)} = W^{(1)^T} $，从而保证这个有两个隐层的DBN的表现至少不比原先的RBM差。

接下来，我们可以在这一“至少不比RBM差”的基础上，对$ W^{(2)} $进行改进。引入近似推断⁴$ Q(h^{(1)} \vert v) $，利用类似于EM算法的方式求DBN的对数似然函数$ \log P(v;\theta) $如下：

\[\begin{align*} \log P(v; \theta) &= \log \sum_{h^{(1)}}P(v, h^{(1)}; \theta) \nonumber\\ &= \log \sum_{h^{(1)}}Q(h^{(1)}\vert v)\frac{P(v, h^{(1)}; \theta)}{Q(h^{(1)}\vert v)} \nonumber\\ &\geq \sum_{h^{(1)}}Q(h^{(1)}\vert v)\left[ \log \frac{P(v, h^{(1)}; \theta)}{Q(h^{(1)}\vert v)}\right] \nonumber\\ &= \sum_{h^{(1)}}Q(h^{(1)}\vert v)[ \log P(v, h^{(1)}; \theta)] + \sum_{h_{(1)}}Q(h^{(1)}\vert v)\left[ \log \frac{1}{Q(h^{(1)}\vert v)}\right] \nonumber\\ &= \sum_{h^{(1)}}Q(h^{(1)}\vert v)[ \log P(v\vert h^{(1)}; W^{(1)}) + \log P(h^{(1)}\vert W^{(2)})] + H(Q(h^{(1)}\vert v)) \label{eq1.18} \end{align*}\]

这里$ H(\cdotp) $是信息熵，第三步的不等号使用了琴生不等式⁵。贪婪学习算法的策略是固定$ W^{(1)} $，并最大化$ \log P(v; \theta) $的下界，即最大化：

\[\begin{equation*} \sum_{h^{(1)}}Q(h^{(1)}\vert v)\log P(h^{(1)}\vert W^{(2)}) \label{eq1.19} \end{equation*}\]

而最大化上式相当于在$ h^{(1)} \sim Q(h^{(1)}\vert v) $时最大化$ \sum_{h^{(1)}}\log P(h^{(1)}\vert W^{(2)}) $。比照RBM的对数似然函数，我们可以注意到，这其实就相当于把第二层看做RBM，把第一层的隐层$ h^{(1)}) $做输入，并最大化该RBM的对数似然函数。于是，我们就可以通过逐层的方式进行训练，每加一层都是对整个DBN的对数似然函数$ \log P(v; \theta) $的下界的提升，如下图所示。

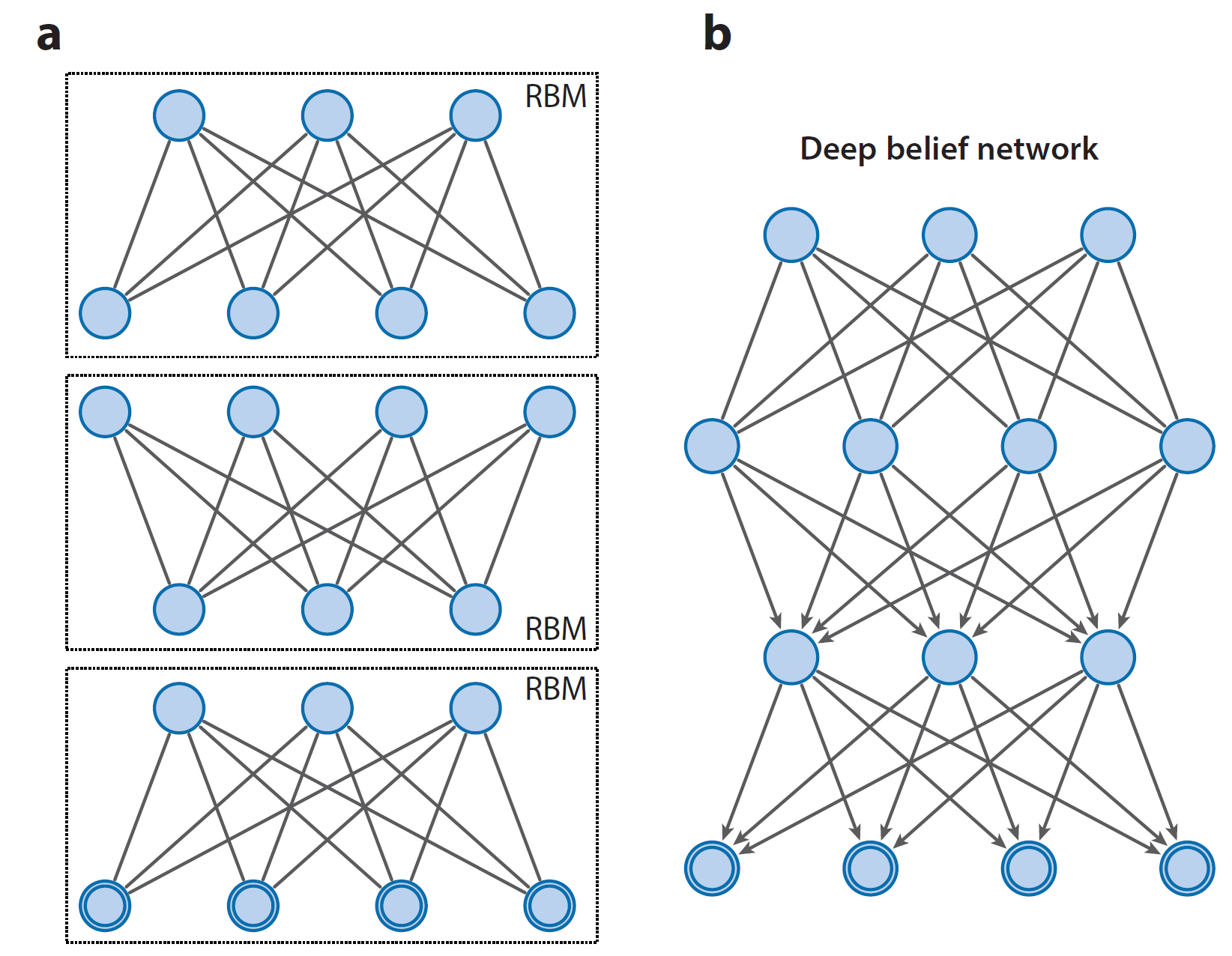
对DBN进行逐层训练，训练时每一层都作为一个RBM。

附录

在RBM取样时，可以利用RBM隐层和显层内的独立性，进行改进的Gibbs Sampling。具体方法为：

• 随机初始化$ y_1, y_2, …, y_N (= h^{(l-1)}, h^{(l)}) $
• 对$ t = 0, 1, 2, … $，循环采样：
  • $ y_i \sim P(y_i\vert v) \forall y_i \in h $
  • $ y_i \sim P(y_i\vert h) \forall y_i \in v $

关于Gibbs Sampling可参考这篇文章

参考

• Ruslan Salakhutdinov. Learning deep generative models. Statistics and Its Application, 2(2):361–385, 2015.

注释